Kvantitative investorer og analytikere mottok for to uker siden den triste nyheten om at Benoit Mandelbrot var død, 85 år gammel.
Mandelbrot pionerte fraktalgeometrien som beskrev at alt som observeres kan brytes ned i mindre komponenter som er identisk med det vi initielt observerte. Dette gjaldt også børskurser.
Lange trender består av mindre trender som har samme karakteristika som de lange trendene. Kortere trender kunne igjen brytes ned i enda kortere bevegelser som også var identisk med den vi hadde observert også videre.
Benoit Mandelbrot var også en pioner innenfor risikoanalyse og mange kjenner til ham nettopp på grunn av dette. I 2004 utgav han boken «The (Mis)behaviour of Markets» sammen med Richard Hudson.
Grunnlaget for de fleste risikoanalyser er historikk. Tidligere erfaringer er således ment å gi oss data for fremtidige hendelser. Dette kan så være, men hva med når det skjer noe som aldri har hent før?
Mandelbrot hevdet at algoritmene som idag benyttes har det til felles at de undervurderer risikoen ved å investere. Ifølge Mandelbrot var det to karaktertrekk ved børsutvikling. Han kalte disse for Joseph og Noah effektene. I førstnevnte som han betegnet som det normale, kunne vi forvente oss at en periode med gode år ble etterfulgt av en periode med dårlige år.
I den andre, Noah, hendte det noe plutselig og katastrofalt. Krakket i 1987, World Trade Center anslaget og, for mange, the Flash Crash 6. mai i år er blant slike.
Risikoalgoritmer modellerer kun førstnevnte ifølge Mandelbrot og dette skjer på tross av at historien viser at Noah situasjoner inntreffer langt oftere enn statistikkbaserte modellene tilsier. Modellene benytter feil forutsetning idet de tar utgangspunkt i at utviklingen vil følge hva man matematisk kaller en «normalfordeling».
I mangel på forståelse for det ukjente, baseres fortsatt de fleste risikoanalyser seg utelukkende på det vi allerede har observert. Vi forventer med andre ord at historien skal gjenta seg.
Observerte svingninger og samvariasjoner danner grunnlaget for det som kalles Value-at-Risk, forkortet til VaR. Vår VaR-faktor er det potensielle investorer oftest spør om. Med det menes hvor store daglige prosentuelle svingninger har vi med en sikkerhet på 95%. Siden fremtiden er ukjent vil man bruke fortiden som pekepinn.
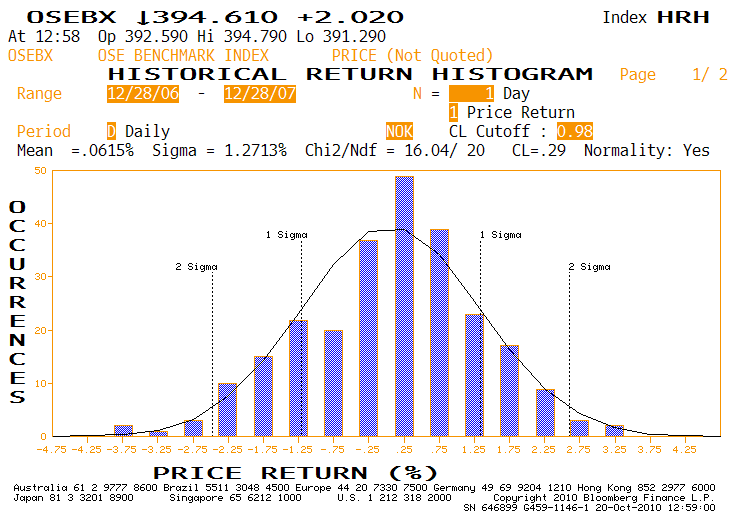
Min sterkt kvantitativtbelastede kollega Øyvind Tvilde gjorde forleden følgende observasjon: I 2007 var det daglige standardavviket på Oslo Børs på 1.27%. Det vil si at i 2 av 3 børsdager befant vi oss innenfor en slik bevegelse målt fra foregående dags slutt. Det var og er helt vanlig å bruke et slikt tall som grunnlag for fremtidige vurderinger av risiko. Man har tross alt rundt et helt år med daglige observasjoner å basere seg på.
Et daglig standardavvik på 1.27% betyr eksempelvis at vi kun står i fare for å oppleve en daglig kursbevegelse på over 5% i én dag i løpet av 90 år. Blant de som baserer seg på dette er både myndigheter og de som låner ut penger til aksjehandel.
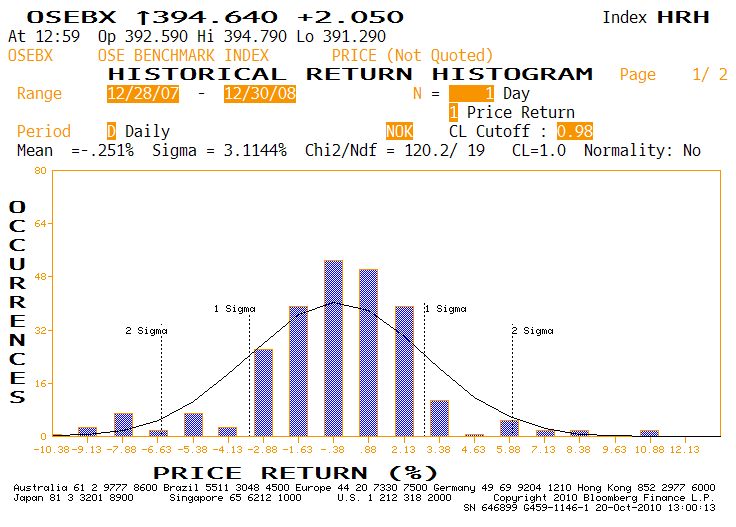
Da støvet hadde lagt seg det påfølgende året, viste det seg at de daglige svingningene hadde vært nesten 2.5 ganger så høye som i 2007. Minst like interessant er det å vite at om man var klarsynt og visste at dette standardavviket skulle bli så høyt, så hjalp heller ikke dette.
Putter man nemlig det daglig observerte standardavviket i 2008 (3.12%) inn i en risikomodell som baserer seg på normalfordeling, får man til svar at en kursbevegelse på over 5% «kun» skal inntreffe på 14 av årets børsdager. Fasiten viste imidlertid at det skjedde 20 ganger – altså 40% oftere enn modellen tilsa etter at det faktisk hadde skjedd!
Nassim Taleb, den risikoopptatte filosofen, tidligere hedgefondsforvalteren og forfatteren, advarte nylig om farene ved å benytte både slike modeller og tenkning gjennom rådet: «Don’t mistake the unobservable for the improbable». Det er dessverre mindre enn 2 år etter den verste finanskrisen siden 30-tallet og allerede lite som tyder på at disse erfaringene og dette rådet i noen særlig grad følges.
Hei Erik. Jeg er helt enig i at markedsaktører bruker et selektivt utsnitt fra historien for å fremme et salgs case. Det verste jeg har sett (uten at dette skal være en konkurranse om nettopp dette) var selgere av eiendomsprosjekter. Fordi det ikke fantes et åpent annenhåndsmarked i disse, skjulte mange selgere det faktum at de hadde overflod av selgere av eksisterende prosjekter til sterkt rabatterte priser, samtidig som de hentet inn nye penger til full pris. Dette er i beste fall tilbakeholdelse av informasjon og i verste fall svindel. Myndighetene har imidlertid overhode ikke engasjert seg.
I kredittobligasjonsmarkedet under finanskrisen var det enkelte meglere som tok enorme spreader (10-20%) mellom det de kjøpte en obligasjon av en kunde for og det de samtidig mottok da solgte den til en annen. Også i dette markedet nyter noen få store goder ved at alle ikke får samme informasjon. Hva gjorde eller gjør Finanstilsynet med dette? Du gjettet det sikkert. Ingenting! /Peter
Hei Tom! Takk for hyggelige ord og også for innspillet. Det finnes opplagte tilpasninger man kan gjøre mht å anvende en mer reell og «curve fitted» distribusjon. Det er også mulig å bruke en implisitt distribusjon utledet av opsjonspriser. Argumentet for en slik vil være at det i det minste er markedets kollektive forventning til sannsynlighetene. Mitt ankepunkt mot VaR er ikke så mye VaR i seg selv, men manges oppfatning at man kan sette to streker under tallet man kommer frem til.
Nassim er åpenbart flink teoretisk men ingen praktiker. Samtidig ville historien og hans markedsmessige ettermæle vært en helt annen dersom finanskrisen inntraff i 2004 og ikke 4 år senere. I 2004 eksisterte fondet hans i beste velgående og både de og han ville ha gjort en kule. I 2008 hadde alle investorene forlatt ham og sjefstraderen hans flyttet til vestkysten (hvor han oppnådde suksessen som egentlig var Nassims).
David Harding (Winton) er en av fysikerne som jeg har stor respekt for og som har klart seg i markedet i lang tid. Han forstår det som Scholes, Merton, Rubinstein etc ikke forstod; nemlig at markeder ikke har ubegrenset likviditet. Det er her interessant å erkjenne at ingen av de 5 forutsetningene i Black & Scholes opsjonsprisingsmodell i realiteten er oppfylt i markedene.
For egen del føler jeg ofte at markedet i mange tilfeller lettere lar seg beskrive gjennom psykologiske enn matematiske modeller. /Peter
Jeg syns dette er trist,Peter.De «sannheter» banknæringen holder seg til er slike optimistiske vurderinger av risiko du argumenterer for er usanne.Disse forer bankselgerne kundene sine med og over tid får man ikke den avkastningen man blir lovet eller risikoen for å tape ventet gevinst er reelt høyere enn antydet.Banknæringen har selvfølgelig interesse av å bygge sin vitenskapelighet på disse løgnene,da selger de mer og har vitenskapen i ryggen.»Vi har ikke gjort noe galt når kundene ikke tjener penger statistisk sett.Dette er vitenskap.»Slik statistikk over tid er nok også bankene forsiktig med å lage.Det er da ikke rettferdig»at de som ikke passer godt nok på pengene» da blir lurt i kvasivitenskapens navn.Bankene innbiller folk at de passer godt på pengene ved å gjøre slik de sier.Enig?En banksannhet var at en fondsinvestering skulle gi gevinst etter 5 år nærmest uansett.Den sannheten er blitt forandret til tyve år.Kanskje står også tyve år for fall?
Hei Peter!
Det er interessant at saa godt som hver gang risikostyring blir diskutert er det svakheter ved normalfordelingen som blir trukket frem. I akademia er det, saa vidt jeg vet, lenge siden man tok i bruk andre fordelinger som underliggende i statistiske modeller. Det er hevet over enhver tvil at normalfordelingen undevurderer «tail risk» og at klasser av fordelinger som f.eks. NIG (Normal-Inversed Gaussian Distributions) er langt bedre underliggende naar man modellerer avkastningen paa finansielle instrumenter som f.eks. aksjer.
Jeg er helt enig at det er svakheter ved de risikostyringsverktoeyene som brukes i dag, men betyr det at man skal erklaere fallitt? Taleb, f.eks., avfeier jo risikostyring naermest helt og holdent, men hva er da saa alternativet? Selv om man godt kan sammenligne modellering med kvalifisert gjetning (og da med betydelige svakheter), er da det tross alt bedre enn alternativet, nemlig ren gjetning.
Spoer du meg er ikke de statistiske/kvantitative utfordringene med modellene det stoerste problemet. Det er langt mer foruroligende at mange av de som bygger disse modellene har veldig god statistisk forstaaelse, men tilsvarende svak oekonomisk forstaaelse. Det blir vanskelig aa vurdere risikoprofilen til en enkelt aktivaklasse dersom du strengt tatt ikke forstaar eksponeringen mot andre aktivaklasser. Det hjelper f.eks. ikke stort aa ha statistiske sofistikerte modeller naar du ikke skjoenner betydningen av at boligmarkedet paa vest-kysten av USA er korrelert med boligmarkedet paa oest-kysten i USA. For all del, jeg har meget stor respekt for quants, men det er utfordringer med aa la doktorer i fysikk og matematikk modellere finansmarkeder.
Tusen takk for en meget lesverdig blogg!
Hei Popper. Muligens er det best å ha et pragmatisk forhold til dette gjennom å si at mangel på risikostyring hos noen, skaper muligheter hos andre. Det sørger i hvert fall for at det skjer formuesøverføringer og kanskje er det en rettferdighet i at de som ikke passer på sine penger heller ikke fortjener å beholde dem.
Det ligger absolutt store gevinster i ytterpunktene og så lenge du er både tålmodig og din egen herre, er det mulig for deg å posisjonere deg for disse. Har man derimot utålmodige investorer (som Nassim Taleb hadde) risikerer man at de alle har bedt om pengene sine tilbake før uttelling skjer.
2/3 av innløsningene vi fikk da aksjemarkedet begynte sin nedgang, skjedde i første fasen av fallet. Begrunnelsen var at «aksjer var så billige». De som kjøpte aksjer opplevde at aksjemarkedet falt 50% fra dette nivået. What can you do? /Peter
Hei Peter!
Dette er spennende! Dette underbygger for at det umulige er langt mer mulig kombinert med et godt MM har mann en dødlig kombinasjon 🙂 All økonomistudenter i dag fores med dette. Det er ingen kritisk tenkning. Vi husker jo hva som skjedde med LTCM. Hva kan ytterste Det er regne broilerfabrikker…. Hva kan konsekvensene bli?
Algoritme handler som tjener penger hver dag har systemer som mangler soliditet, et slikt system varer ikke evig. Da er det bedre risk management etter steinaldermetoden! Det som er spennende er at de store gevinstene ligger i ytterpunktene, ihvertfall for meg 🙂